Quadratic spline interpolation and Bezier curve theories visualizer.
In the mathematical field of numerical analysis, spline
interpolation is a form of interpolation where the interpolant is a
special type of piecewise polynomial called a spline.
You can read the full article of the spline interpolation on wiki.
A Bézier curve is a parametric curve used in computer graphics and
related fields. The curve, which is related to the Bernstein
polynomial, is named after Pierre Bézier, who used it in the 1960s for
designing curves for the bodywork of Renault cars. Other uses include
the design of computer fonts and animation.
You can read the full article of the Bézier curve on wiki.
This project is an implementation of the spline interpolation and Bézier curve theories.
The application takes some coordinates then calculates it’s quad equation and finally visualize the graphs using Bézier curve.
Main feature of the application is that you can control the animation speed and the drawing steps, also you can generate the quadratic equations of some points.
Let’s assume that we have the following points from 0 to n:
What we need is to connect every two points with a quad curve as following:
We can see that we have n + 1 points, and actually if we want to connect every two
points then we will need n equation.
So we can conclude that:
number of equations = number of points - 1
At first you need to know that the general equation of quadratic function is as following:
f(x) =
So the equations we have are:
.\
.\
.
We will notice that we have 3 unknowns a, b, and c in every equation, so to calculate them we need three equation from the same equation to solve them and calculate the unknowns, so we need 3n equations.
Luckily we already know two points values for every equation for ex:
lest assume the first point is (10, 11) and the second one is (12, 15) so we have
As we can see we need one more equation to define a,b, and c for every quadratic equation.
Now we need a relation between the curves to conclude the unknowns,
let’s think about the differentiation what if we differentiate the curve equation ?
We will get an equation that gives us the slope at any point on the curve.
Actually we can notice that every two curves have a joint point between them,
so we can assume that the slope at that point is the same.
So we can conclude that the differentiation of the curve i equals the differentiation of the curve i + 1.
let’s simplify:
Now after that assumption we have 3n - 1 because of the first two points we don’t know what is the slope of the point (X0, Y0), so we need one more equation.
What if we assumed that the first equation is a linear equation ?
We will get rid of one unknown right ?
So actually after that another assumption we need 3n - 1 equations, and we already have those equations.
Let’s just simplify the first line equations:
We assumed that the first two points connects with a line so we can say that a[0] = 0, then the new equations are:
Subtract the two equations:
)
and we can also conclude that
)
Finally now we can calculate the rest of the quadratic equations unknowns using these three equations:
In the Quadratic Bézier curve all what we need to draw the curve is three points:
SPCPEP
So how we can draw the curve using these three points ?
We will connect the SP with the CP using a line let’s call it L1,
and connect the CP with the EP using another line let’s call it L2 as following:

Now the main idea of the Bézier curve is that if we moved by some ratio of L1
and we moved the same ratio of L2 we will get two points that we can connect them by a third line let’s call it L3.
In fact if we moved the same ratio of L3 we will get a point, and the interesting thing is that this point is on the curve that we are trying to draw.
If we repeated this step by different ratios we will get some points that we can connect them to draw the curve as following:
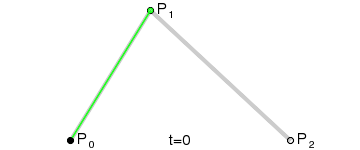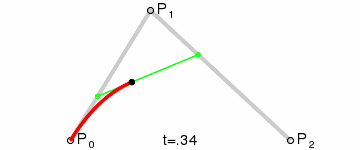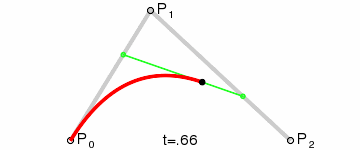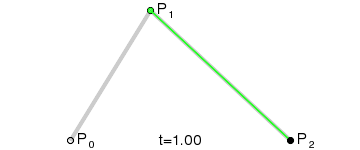
In the previous gif we can see that t represents the current ratio, and the more the ratio step value was smaller the more the curve will be smoother.
Now how we can calculate the curve point at t ?
Let’s say that SP = (Xs, Ys), CP = (Xc, Yc), and EP = (Xe, Ye).
We now want to calculate the point on L1 at t.
From the following image:

let’s call the angle RX by theta, what if we take the cos of that theta ?
We will get the following equation:
&space;=&space;\frac{X}{R}&space;=&space;\frac{x}{r})
let’s call the previous equation by Eq1.
So what is next ?
Actually we already know that at ratio t, r will equal t . R so
let’s call previous equation by Eq2.
From Eq2 into Eq1:
So we can conclude that Xv = Xs + x.
From the same steps but by using sin(theta) we can conclude that:
So Yv will be:
Yv = Ys + y
Now what does Y and X equals ?X is the difference between Xc and Xs, and Y is the difference between Yc and Ys.
X = Xc - Xs
Y = Yc - Ys
So finally the important equations will be:
)
)
Now we want to calculate the point on L2 at t.
From the following image:

Like the last step we will take cos and sin to the YR angle, and we will conclude that:
)
)
Finally we want to get the point that on the L3 line.
From the following image:

from the previous derives we can say:
)
)
After some simplification we can say:
&space;+&space;2t(Xc&space;-&space;Xs)&space;+&space;Xs)
&space;+&space;2t(Yc&space;-&space;Ys)&space;+&space;Ys)
We know that to draw a Bézier curve we need 3 points start, end, and control,
in this case we already know the start and the end points of the curve, all what we need now is to get the control point.
The control point of the curve is the cross point of the tangent lines of the first and end points.
So how we can get the tangent line equation ?
As we know if we differentiate the curve equation we will get an equation that gives us the slope at any point on the curve right ?
We can get the slope at the first and end points, then from them we can conclude two linear equation and solve them to get the cross point.
So we can say that:
m1 =
m2 =
Note that the general form for any linear equation is y = mx + b.
Then the first line equation will be:
y = m1 x + b1
and the second line equation is:
y = m2 x + b2
We already calculated m1 and m2, we need now to calculate b1 and b2.
What we can do to calculate b1 and b2 ?
Actually we know a point (start point) on the first line and a point (end point) on the second line right ?
So we can calculate b1 and b2 from them.
Now we need to solve the two lines equations to get the cross point:
)
&space;+&space;b_1)
After some simplification we can say:
&space;+&space;b(X_s-X_e)}{2a(X_s&space;-&space;X_e)})
(\frac{Ye&space;-&space;Ys&space;+&space;2a(X_s^2&space;-&space;X_e^2)&space;+&space;b(X_s&space;-&space;X_e)}{2a(X_s&space;-&space;X_e)}&space;-&space;X_s)&space;+&space;Y_s)
Number of quadratic equations = number of points - 1
We will assume that the first equation is a linear equation, So:
)
The equation to conclude the rest of the quadratic equations:
To draw Bézier curve we need three points start, end and control.
To get the curve point at a ratio t we can use the following equations:
&space;+&space;2t(Xc&space;-&space;Xs)&space;+&space;Xs)
&space;+&space;2t(Yc&space;-&space;Ys)&space;+&space;Ys)
To convert a quad equation to a Bézier curve we need to calculate the control point, and we can do that with the following equations:
&space;+&space;b(X_s-X_e)}{2a(X_s&space;-&space;X_e)})
(\frac{Ye&space;-&space;Ys&space;+&space;2a(X_s^2&space;-&space;X_e^2)&space;+&space;b(X_s&space;-&space;X_e)}{2a(X_s&space;-&space;X_e)}&space;-&space;X_s)&space;+&space;Y_s)





